What is two’s complement and how do convert decimals and binary numbers into two’s complement?

Table of Contents

The term “two’s complement” is a very well-known term in the binary number system. It is used to perform different arithmetic operations like addition, subtraction, and multiplication. It is the easiest way to represent signed integers on a computer.
Table of Contents
Usually, this method is used to encode negative numbers because it is easy to encode positive numbers but it is complex to encode negative numbers so that is the reason, we use two’s complement.
In this article, we will study the basic definition of two’s complement, methods of finding two’s complement, and how to convert a decimal number into a binary number. We will also study the conversion of binary numbers into two’s complements.
Definition:
According to Wikipedia:
Two’s complement is a mathematical operation on binary numbers, it is used in computer science as a method of signed number representation. When the Most Significant Bit is a one, the number is signed as negative.
How to find the two’s complements of binary and decimal numbers?
There are many ways to find two’s complements. If you have to find the two’s complement of any decimal number, you should have to convert it first.
The binary number system contains only two digits 0 and 1. We communicate with the computer with the help of a binary number system because computers only understand binary language.
Conversion of decimals into two’s complement
There is a simple procedure for converting a decimal number into a binary number. The following examples will be helpful for you in converting any decimal number into a binary number.
Example#1:
Convert “17” into the binary number system and take its two’s complement.
Solution:
Step-1:
Draw a table and start dividing the number with the base to which you want to convert it. As we are going to convert “17” into the binary system which is also known as the system whose base is “2”
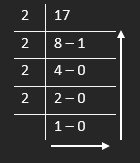
After dividing, you should know how to write the answer. Right the answer in the direction of arrows. Start from the bottom left then write the value which is next to it and after that move vertically upward in the table and write the corresponding values.
The binary of “17” is “10001”
Step-II:
Complete the bits of the given decimal number. The range of 6-bits is between -32 to 31 and the answer consists of 5-bits, so firstly we will complete the bits.
Completing bits:
0 1 0 0 0 1
Step-III:
Taking One’s complement of 0 1 0 0 0 1
Inverting all the values (replacing 0’s by 1’s and 1’s by 0’s)
1 0 1 1 1 0
Step-IV:
Taking two’s complement by adding 1 in the inverted value.
10 11 10
+ 1
10 11 11
1 0 1 1 1 1 Answer.
Answer table:
| Decimal value | 17 |
| Binary value | 1 0 0 0 1 |
| Two’s complement | 1 0 1 1 1 1 |
Example#2:
Convert “1254” into the binary number system and take its two’s complement.
Solution:
Step-I:
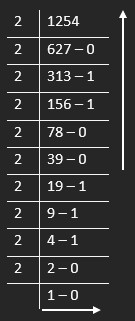
The binary number of “1254” is “10011100110”
Step-II: Complete the bits.
The range of 12-bits is between -2048 to 2047 and the answer consists of 11-bits. So, firstly we will complete the bits.
After completing bits, we got:
0 1 0 0 1 1 1 0 0 1 1 0
Step-III: Taking One’s complement.
0 1 0 0 1 1 1 0 0 1 1 0
Step-IV: Add “1” to the inverted value.
0100 1110 0110
+ 1
1 100 1110 0111
1 1 0 0 1 1 1 0 0 1 1 1 Answer.
Answer Table:
| Decimal value | 1254 |
| Binary value | 1 0 0 1 1 1 0 0 1 1 0 |
| Two’s complement | 1 1 0 0 1 1 1 0 0 1 1 1 |
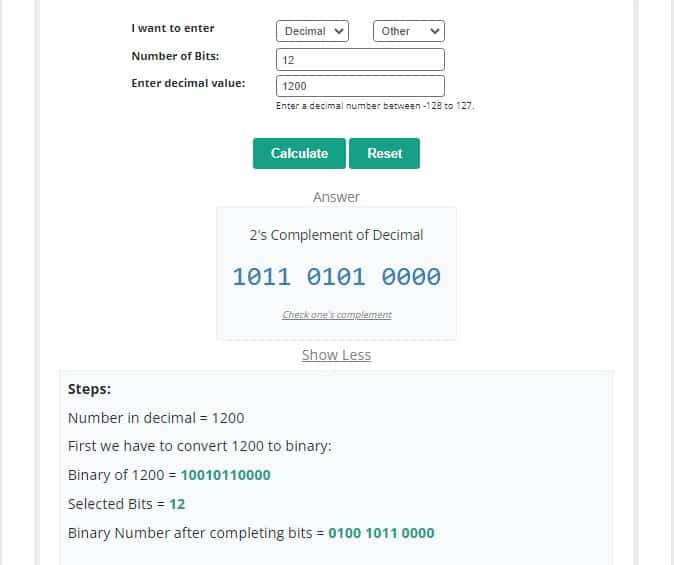
To get rid of these long calculations, you can use a 2’s complement calculator to get the result in a couple of seconds.
Steps to use this calculator.
- Select the input type.
- Enter the number of bits.
- Enter the value.
- Click on the calculate button to see the step-by-step result.
Conversion of binary numbers into two’s complement
To take the two’s complement of a binary number follow the following steps.
- Invert all the values of the given binary number (Take one’s complement)
- Add “1” to the inverted number.
The following examples will be helpful for you to understand the procedure.
Example#1:
Take the Two’s complement of 1010101.
Solution:
Step-I: Taking One’s complement of 1 0 1 0 1 0 1
Inverting all the values (Replacing 0’s by 1’s and 1’s by 0’s) we get:
0 1 0 1 0 1 0
Step-II: Adding “1”
1 0 1 0 1 0 1
+ 1
0 1 0 1 0 1 1
0 1 0 1 0 1 1 Answer.
Answer Table:
| Decimal value | 15 |
| Binary value | 1 1 1 1 |
| Two’s complement | 1 1 0 0 0 1 |
Summary
In this article, we have discussed the basic theory of the two’s complement. We also discussed the method of solving the two’s complement and how to calculate it using an online calculator. You have witnessed that two’s complement is not a difficult topic, now you can easily solve the problems related to two’s complement.